高考必刷卷2023年全国高考名校名师联席名制(新高考)信息卷(五)5数学试卷 答案(更新中)

高考必刷卷2023年全国高考名校名师联席名制(新高考)信息卷(五)5数学试卷答案,我们目前收集并整理关于高考必刷卷2023年全国高考名校名师联席名制(新高考)信息卷(五)5数学得系列试题及其答案，更多试题答案请关注我们

高考必刷卷2023年全国高考名校名师联席名制(新高考)信息卷(五)5数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

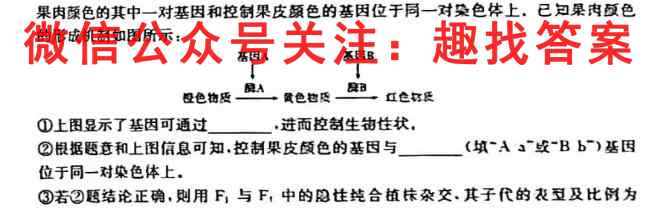
B橙色物及黄色物质红色打氏①上图显示了基因可通过,进而控制生物性状,②根据题意和上图信息可知,控制果皮颜色的基因与(填Aa或Bb.^)基因位于同一对染色体上.

分析（1）求得函数的导数，求得切线的斜率和切点，解方程可得a，b，进而得到f（x）的解析式；
（2）求出f（x）的导数，求得单调区间和极值，结合图象，即可得到方程解的情况．

解答解：（1）∵函数$f（x）=\frac{1}{3}{x^3}+a{x^2}-bx+4$，
f’（x）=x²+2ax-b，
根据题意得f’（2）=4，即4a-b=0，
又$f（2）=8-\frac{10}{3}$，即有$\frac{8}{3}$+4a-2b+4=8-$\frac{10}{3}$，
解得$a=\frac{1}{2}，b=2$，
∴$f（x）=\frac{1}{3}{x^3}+\frac{1}{2}{x^2}-2x+4$；
（2）∵$f（x）=\frac{1}{3}{x^3}+\frac{1}{2}{x^2}-2x+4$，
∴f’（x）=x²+x-2=（x+2）（x-1），
令f’（x）＞0解得x＜-2或x＞1，f’（x）＜0解得-2＜x＜1，
即有f（x）的增区间为（-∞，-2），（1，+∞），减区间为（-2，1），
即有x=1处取得极小值，且为$\frac{17}{2}$，x=-2处取得极大值，且为$\frac{22}{3}$．
则当k＜$\frac{17}{6}$或k＞$\frac{22}{3}$时，方程k=f（x）有一个解；
当k=$\frac{17}{6}$或k=$\frac{22}{3}$时，方程k=f（x）有两个解；
当$\frac{17}{6}$＜k＜$\frac{22}{3}$时，方程k=f（x）有三个解．

点评本题考查导数的运用：求切线的斜率和单调区间、极值，考查数形结合的思想方法，以及运算能力，属于中档题．

高考必刷卷2023年全国高考名校名师联席名制(新高考)信息卷(五)5数学