衡中同卷2022-2023上学期高三五调(新高考/新教材版)数学试卷答案,我们目前收集并整理关于衡中同卷2022-2023上学期高三五调(新高考/新教材版)数学得系列试题及其答案,更多试题答案请关注我们

衡中同卷2022-2023上学期高三五调(新高考/新教材版)数学试卷答案
以下是该试卷的部分内容或者是答案亦或者啥也没有,更多试题答案请关注微信公众号:趣找答案/直接访问www.qzda.com(趣找答案)
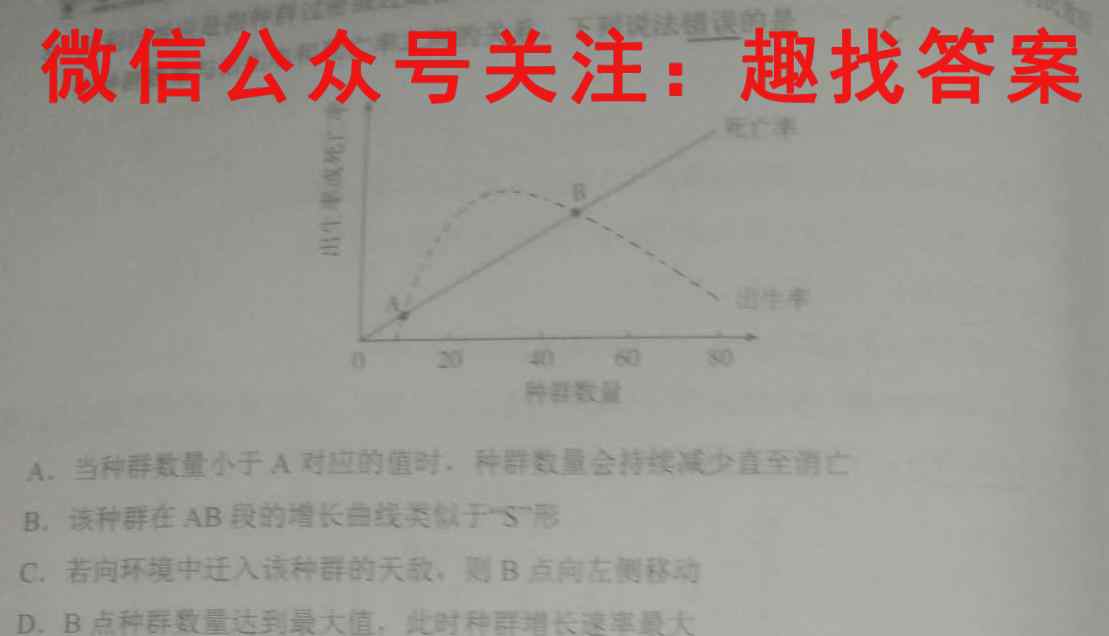
之间的关系。下列说法错误的是C2040种群数量A、当种群数量小于A对应的值时,种群数量会持续减少直至消亡B.该种群在AB段的增长曲线类似于“S形C.若向环境中迁入该种群的天敌,则B点向左侧移动D.B点种群数量达到最大值,此时种群增长速率最大
分析(1)化简得f(x)=cos(2x+$\frac{π}{3}$),令2x+$\frac{π}{3}$=$\frac{π}{2}$+kπ,解出对称中心,令-π+2kπ≤2x+$\frac{π}{3}$≤2kπ,解出单调增区间;
(2)由f(A)+1=0解出A,由b+c=2得b2+c2=(b+c)2-2bc=4-2bc,代入余弦定理得a2=4-3bc,即bc取得最大值时,a2取得最小值.
解答解:(1)f(x)=cos2x-$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$=$\frac{1}{2}$cos2x-$\frac{\sqrt{3}}{2}$sin2x=cos(2x+$\frac{π}{3}$),
令2x+$\frac{π}{3}$=$\frac{π}{2}$+kπ,解得x=$\frac{π}{12}$+$\frac{kπ}{2}$,
∴f(x)的对称中心为:($\frac{π}{12}$+$\frac{kπ}{2}$,0),
令-π+2kπ≤2x+$\frac{π}{3}$≤2kπ,解得-$\frac{2π}{3}$+kπ≤x≤-$\frac{π}{6}$+kπ,
∴f(x)的单调递增区间为:[-$\frac{2π}{3}$+kπ,-$\frac{π}{6}$+kπ],k∈Z.
(2)∵f(A)+1=0,即cos(2A+$\frac{π}{3}$)+1=0,∴cos(2A+$\frac{π}{3}$)=-1.
∵0<A<π,∴$\frac{π}{3}$<2A+$\frac{π}{3}$<$\frac{7π}{3}$,
∴2A+$\frac{π}{3}$=π,∴A=$\frac{π}{3}$.
∵b+c=2,∴b2+c2=(b+c)2-2bc=4-2bc
∴a2=b2+c2-2bc•cosA=4-3bc≥4-3($\frac{b+c}{2}$)2=1.
当且仅当b=c=1时,a取得最小值1.
点评本题考查了三角函数的恒等变换和性质,余弦定理得应用,是中档题.

衡中同卷2022-2023上学期高三五调(新高考/新教材版)数学
 答案联动网
答案联动网