在四边形ABCD中,AC=AB,DC=DB,∠CAB=60°,∠CDB=120°,E是AC上一点,F是AB延长线上一点,且CE=BF.
(1)在图1中,求证:DE=DF;
(2)在图1中,若点G在AB上且∠EDG=60°,试猜想CE,EG,BG之间的数量关系并证明;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:如图2,在四边形ABCD中,∠ABC=90°,∠CAB=∠CAD=30°,点E在AB上,DE⊥AB,且∠DCE=60°,若AE=3,求BE的长.
考点:全等三角形的判定与性质,勾股定理
专题:
分析:(1)根据全等三角形的判定与性质,可得∠C=∠DBA,根据全等三角形的判定与性质,可得DE与DF的关系;
(2)根据全等三角形的性质,可得DF=DE,∠CDE=∠BDF,再根据全等三角形的判定与性质,可得EG=FG=GB+BF;
(3)根据全等三角形的性质,可得AM=AB,CM=BC,根据直角三角形的性质,可得AD的长,根据线段的和差,可得答案.
(2)根据全等三角形的性质,可得DF=DE,∠CDE=∠BDF,再根据全等三角形的判定与性质,可得EG=FG=GB+BF;
(3)根据全等三角形的性质,可得AM=AB,CM=BC,根据直角三角形的性质,可得AD的长,根据线段的和差,可得答案.
解答:(1)解:如图1,连接AD,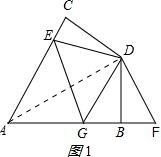
在△ACD和△ABD中,
|
|
|
,
∴△ACD≌△ABD(SSS)
∴∠C=∠DBA.
又∵∠CAB=60°,∠CDB=120°,
∴∠C=∠DBA=∠DBF=90°.
在△DCE和△DBF中,
|
|
|
,
∴△ECD≌△FBD(SAS)
∴DE=DF.
(2)由(1)知△ECD≌△FBD,
∴DF=DE,∠CDE=∠BDF.
又∵∠CDE+∠GDB=∠CDB-∠EDG=120°-60°=60°
∴∠EDG=∠FDG.
在△EGD和△FGD中,
|
|
|
,
∴∴△EGD≌△FGD(SAS)
∴EG=FG=GB+BF,
∴EG=CE+BG;
(3)如图2: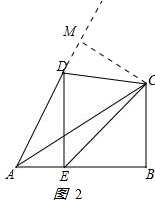
过C作CM⊥AD交AD的延长线于M,
在△AMC和△ABC中,
|
|
|
,
∴△AMC≌△ABC(AAS)
∴AM=AB,CM=BC,
由以上可知DM+BE=DE.
∵AE=3,∠AED=90°∠DAB=60°,
∴AD=6.
由勾股定理得:DE=3
|
|
3 |
∴DM=AB-6=BE+3-6=BE-3,
∴BE-3+BE=3
|
|
3 |
即BE=
3+3
|
||
| 2 |
.
点评:本题考查了全等三角形的判定与性质,利用了全等三角形的判定与性质,直角三角形的性质.
 答案联动网
答案联动网