承德市2022~2023学年高一第二学期期末考试(23-542A)数学试卷 答案(更新中)

承德市2022~2023学年高一第二学期期末考试(23-542A)数学试卷答案,我们目前收集并整理关于承德市2022~2023学年高一第二学期期末考试(23-542A)数学得系列试题及其答案，更多试题答案请关注我们

承德市2022~2023学年高一第二学期期末考试(23-542A)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

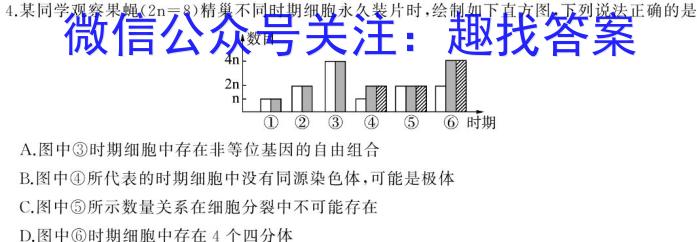
4.某同学观察果蝇(2n=8)精巢不同时期细胞永久装片时,绘制如下直方图,下列说法正确的是A.图中③时期细胞中存在非等位基因的自由组合B.图中④所代表的时期细胞中没有同源染色体,可能是极体C.图中⑤所示数量关系在细胞分裂中不可能存在D.图中⑥时期细胞中存在4个四分体

分析（Ⅰ）由题意设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0），由已知可得a²-b²=1，$\frac{1}{2}（2a）b=\sqrt{2}$，联立求得a，b的值，则椭圆方程可求；
（Ⅱ）由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0），利用椭圆的通径长结合a²-b²=1求得a，b的值，再由隐含条件求出c，则椭圆的离心率可求．

解答解：（Ⅰ）由题意设椭圆方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0），
则有a²-b²=1，$\frac{1}{2}（2a）b=\sqrt{2}$，
解得$a=\sqrt{2}$，b=1，
∴椭圆C的方程为$\frac{{x}^{2}}{2}+{y}^{2}=1$；
（Ⅱ）由题意设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0），
则有$\frac{2{b}^{2}}{a}=3$，又a²-b²=1，∴2a²-3a-2=0，
解得：a=2或a=-$\frac{1}{2}$（舍）．
∴b²=a²-1=3，c²=a²-b²=4-3=1，则c=1．
∴椭圆C的离心率$e=\frac{c}{a}=\frac{1}{2}$．

点评本题考查椭圆的简单性质，考查了椭圆方程的求法，是中档题．

承德市2022~2023学年高一第二学期期末考试(23-542A)数学