2022-2023学年山东省高二质量检测联合调考(23-504B)数学试卷 答案(更新中)

2022-2023学年山东省高二质量检测联合调考(23-504B)数学试卷答案,我们目前收集并整理关于2022-2023学年山东省高二质量检测联合调考(23-504B)数学得系列试题及其答案，更多试题答案请关注我们

2022-2023学年山东省高二质量检测联合调考(23-504B)数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

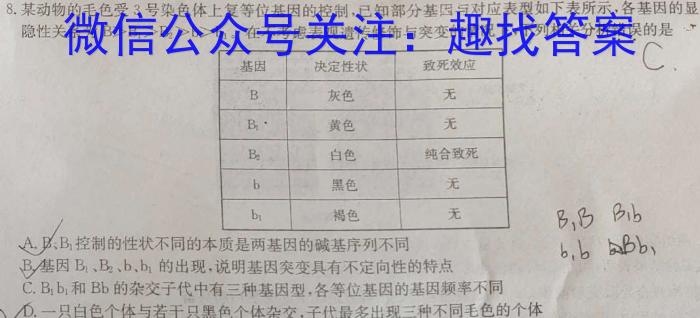
8.某动物的毛色受3号染色体上复等位基因的控制,已知部分基因与对应表型如下表所示,各基因的显隐性关系为B>B1>B2>b>b1。,在不考虑表观遗传修饰与突变的情况下,下列相关分析错误的是CA.D:B1控制的性状不同的本质是两基因的碱基序列不同6.6Bb,BB1、B2、b、b1的出现,说明基因突变具有不定向性的特点C.B1b1和Bb的杂交子代中有三种基因型,各等位基因的基因频率不同D.一只白色个体与若干只黑色个体杂交,子代最多出现三种不同毛色的个体

分析（1）由已知条件利用分层抽样的性质能求出从三个工作组中分别抽取的人数．
（2）从抽取的5名代表中再随机抽取2名参与意见稿的修改工作，先求出基本事件总数，再求出这两名中没有A组人员包含的基本事件个数，由此能求出这两名中没有A组人员的概率．

解答解：（1）∵三个工作组A、B、C，分别有组员36人、36人、18人．
现采用分层抽样的方法从A、B、C三个工作组中抽取共5名代表，
∵A组应该抽取：$36×\frac{5}{36+36+18}$=2人，
B组应该抽取：$36×\frac{5}{36+36+18}$=2人，
C组应该抽取：$18×\frac{5}{36+36+18}$=1人．
（2）从抽取的5名代表中再随机抽取2名参与意见稿的修改工作，
基本事件总数n=${C}_{5}^{2}$=10，
这两名中没有A组人员包含的基本事件个数m=${C}_{3}^{2}$=3，
∴这两名中没有A组人员的概率p=$\frac{m}{n}$=$\frac{3}{10}$．

点评本题考查分层抽样的应用，考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

2022-2023学年山东省高二质量检测联合调考(23-504B)数学