安徽省2022-2023学年度八年级下学期阶段评估（二）【7LR-AH】数学试卷 答案(更新中)

安徽省2022-2023学年度八年级下学期阶段评估（二）【7LR-AH】数学试卷答案,我们目前收集并整理关于安徽省2022-2023学年度八年级下学期阶段评估（二）【7LR-AH】数学得系列试题及其答案，更多试题答案请关注我们

安徽省2022-2023学年度八年级下学期阶段评估（二）【7LR-AH】数学试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注微信公众号：趣找答案/直接访问www.qzda.com(趣找答案)

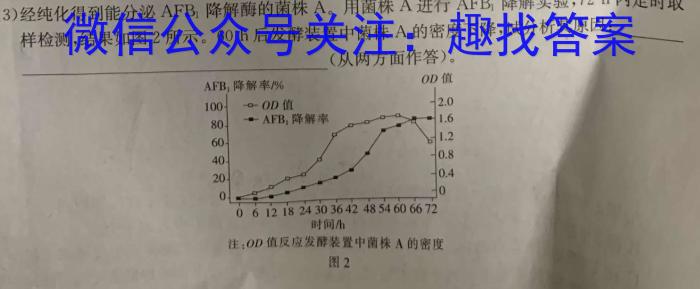
(3)经纯化得到能分泌AFB1行降解酶的菌株A。用菌株A进行AFB1降解实验,72h内定时取样检测,结果如图2所示。60h后发酵装置中菌株A的密度下降,试分析其原因:(从两方面作答)。时间/h注:OD值反应发酵装置中菌株A的密度图2

分析画出正弦函数图象，数形结合可得答案．

解答解：作出函数y=sinx的图象，如图所示：

由图可得：（1）sinx≥$\frac{1}{2}$时，x∈[$\frac{π}{6}$+2kπ，$\frac{5π}{6}$+2kπ]，k∈Z，即原不等式的解集为[$\frac{π}{6}$+2kπ，$\frac{5π}{6}$+2kπ]，k∈Z；
（2）sinx≤$\frac{1}{2}$时，x∈[$\frac{5π}{6}$+2kπ，$\frac{13π}{6}$+2kπ]，k∈Z，即原不等式的解集为[$\frac{5π}{6}$+2kπ，$\frac{13π}{6}$+2kπ]，k∈Z；
（3）sin（x+$\frac{π}{6}$）≥$\frac{\sqrt{3}}{2}$时，x+$\frac{π}{6}$∈[$\frac{π}{3}$+2kπ，$\frac{2π}{3}$+2kπ]，k∈Z，即x∈[$\frac{π}{6}$+2kπ，$\frac{π}{2}$+2kπ]，k∈Z，即原不等式的解集为[$\frac{π}{6}$+2kπ，$\frac{π}{2}$+2kπ]，k∈Z；
（4）sin（x+$\frac{π}{6}$）≤$\frac{\sqrt{3}}{2}$时，x+$\frac{π}{6}$∈[$\frac{2π}{3}$+2kπ，$\frac{7π}{3}$+2kπ]，k∈Z，即x∈[$\frac{π}{2}$+2kπ，$\frac{13π}{6}$+2kπ]，k∈Z，即原不等式的解集为[$\frac{π}{2}$+2kπ，$\frac{13π}{6}$+2kπ]，k∈Z；

点评本题考查的知识点是正弦函数的图象，三角不等式的解法，难度中档．

安徽省2022-2023学年度八年级下学期阶段评估（二）【7LR-AH】数学